Confusion matrix 是一個 NxN 的矩陣,可用來呈現分類模型 (Classification Models) 的結果,本篇除了介紹混淆矩陣外,還會介紹 Accuracy, Recall, Precision, F-score 是什麼,以及在面對分類問題時,如何選擇這些衡量分類指標。
Table
Confusion matrix
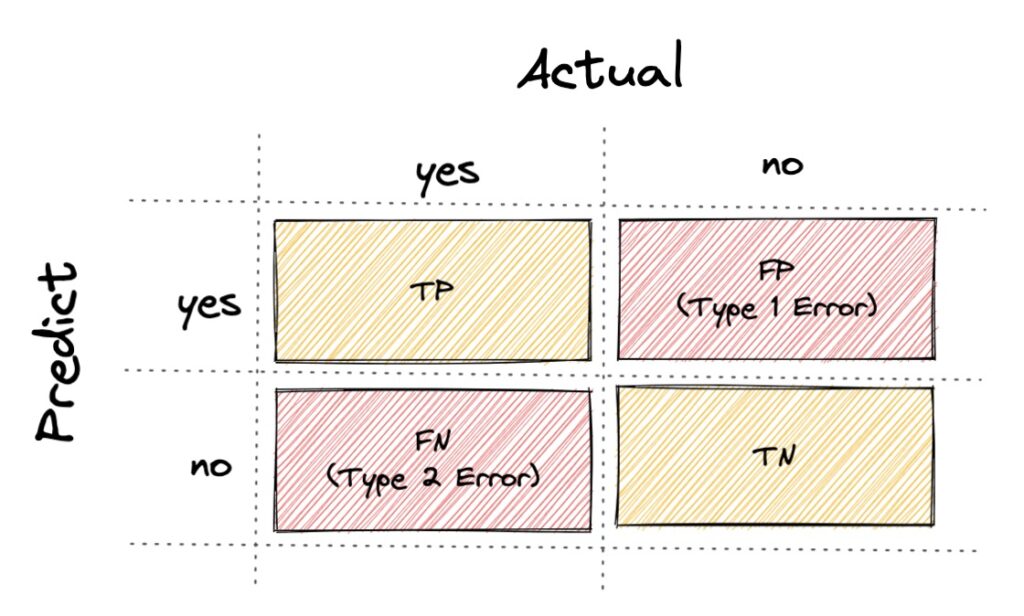
首先我們從最簡單的二元分類來看,假設今天的分類問題只有兩類 (正常信件 or 廣告信件),那預測出來的結果會有四種 (如下):
- TP: 實際是正常信件,且預測結果是正常
- TN: 實際是廣告信件,且預測結果是廣告
- FP: 實際是廣告信件,且預測結果是正常 (Type 1 Error)
- FN: 實際是正常信件,且預測結果是廣告 (Type 2 Error)
Accuracy
- Accuracy 公式: (TP + TN)/(TP + TN + FP + FN)
- Accuracy 是最常見的分類指標,但在分類結果分布不均的情況下,這個評估是會有缺陷。舉例如果樣本數裡面有 90% 的結果都是正常信件,有一個模型將所有的預測都回答是正常信件,那準確率會達到 90%,看起來有很高的預測性,但其實存在著缺陷。所以當樣本分類分布不均的話,可以使用接下來介紹的 Precision 和 Recall。
Recall
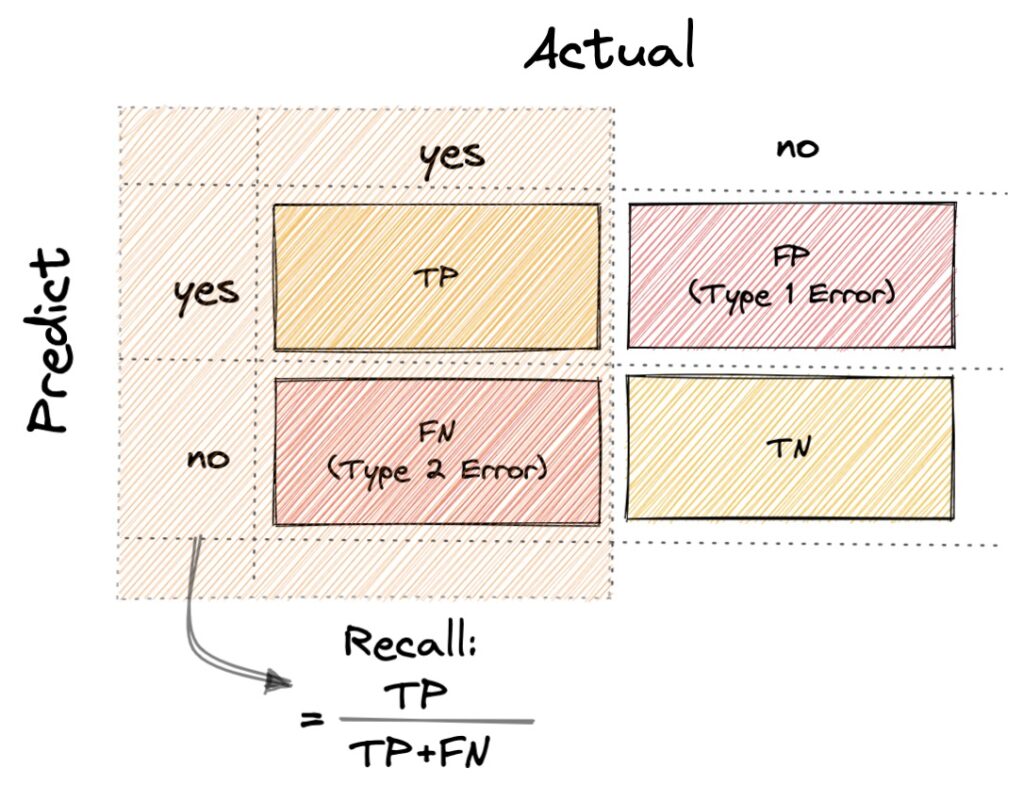
- Recall 公式: TP/(TP + FN)
- 在分類信件問題時,我們會盡量避免正常的信件被分類到廣告信件,因為如果阻擋了使用者重要信件的話,會造成使用者的體驗很差,而 FN 代表著當實際結果是正常信件,而預測分類為廣告信件的類別,所以當我們要避免 FN (type2 error) 的情況發生時,我們會使用 Recall 來衡量預測結果。
Precision
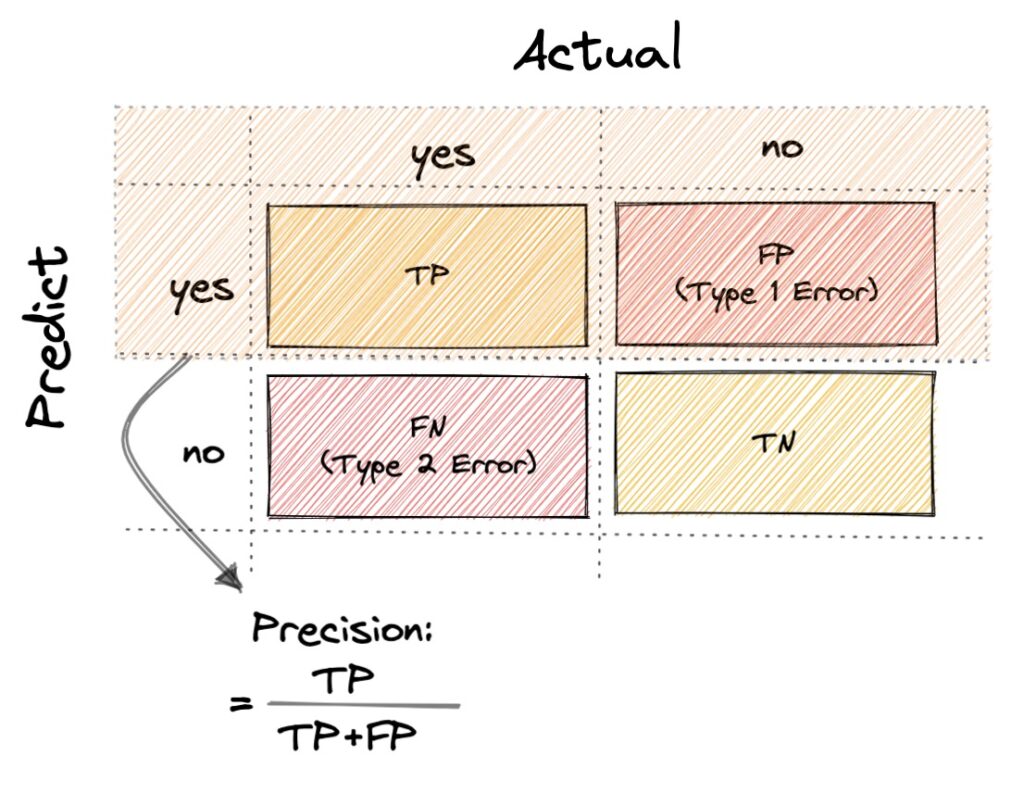
- 公式:Precision = TP/(TP + FP)
- FP (type 1 error) 代表著實際結果是錯誤,而預測結果是正確,假設今天是面對門禁的分類問題時,如果讓壞人可以通過門禁的檢測,那會造成很嚴重的影響。所以當我們要避免 FP (type 1 error) 的情況發生時,我們會使用 Precision 來衡量預測結果。
F-score
- F-score 可以看作是 Recall 和 Precision 的加權平均,當我們認為 Recall 較為重要時 β 可以設定為大於 1,而當 Precision 較為重要時 β 可以設定為等於 1
- F1-score,β 設定為 1 時,則 Recall 和 Precision 的加權趨近於相等,所以算出的值接近於兩者的平均
- F1-score 公式: 2 * precision * recall/(precision + recall)
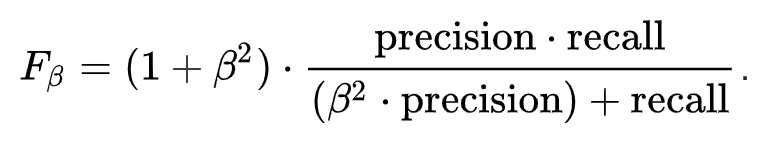
實際演練題
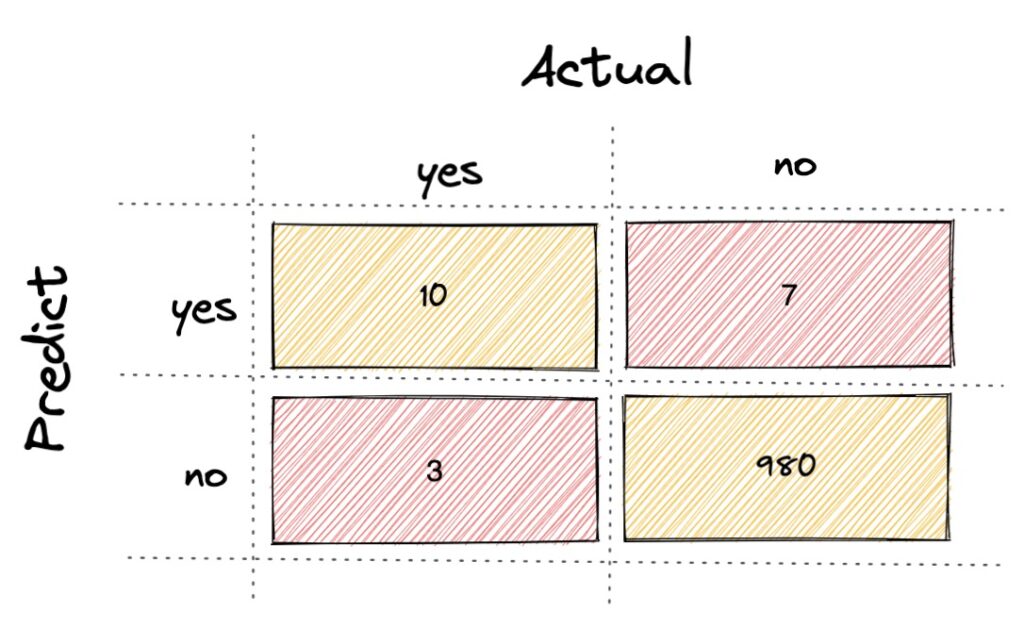
假設今天有樣本數 1000 筆:
- TP: 有 10 筆被預測出是廣告信件,實際上也是廣告信件
- TN: 有 980 筆被預測是正常信件,實際上也是正常信件
- FP: 有 7 筆被預測出廣告信件,實際上是正常信件
- FN: 有 3 筆被預測是正常信件,實際上是廣告信件
- Accuracy (TP + TN)/(TP + TN + FP + FN) = 990/1000 = 99%
- Recall TP/(TP + FN) = 10/13 = 76%
- Precision TP/(TP + FP) = 10/17 = 58%
- F1-score (2 * precision * recall/(precision + recall)) = 66%
如果採用 Accuracy,99% 準確率看起來很精準,但因為分類過於偏差所以,但實際上並不適合使用,而信件分類問題會比較注重 FN (type 2 error),所以最適合使用 Recall 來當衡量標準。
